Accueil > Recherche / Enseignement > Recherche > Thèse > Introduction aux Réseaux de Neurones
 Introduction aux Réseaux de Neurones
Introduction aux Réseaux de Neurones
samedi 19 juillet 2003, par
1. ) Introduction
2. ) Neurones Biologiques
3. ) Approches Formelles
-
3.1. ) Neurone formel
-
3.2. ) Les réseaux de neurones formels
-
3.3. ) Le perceptron
-
3.4. ) Les réseaux de neurones récurrents
-
3.5. ) Conclusion
4. ) La Commande Neuronale
5. ) Conclusion
1. ) Introduction
Le cerveau humain est considéré comme le siège de l’intelligence, de la créativité, de l’émotivité, de la conscience et de la mémoire. Très tôt l’homme s’est intéressé à cet objet complexe : déjà en Egypte, au temps des pharaons, les médecins prêtaient une attention particulière à cet organe. Depuis, de nombreux chercheurs ont essayé de percer le secret de son mode de fonctionnement. Le connexionnisme est la version technologique de cette recherche. Cette première partie présente un rapide aperçu de ces techniques connexionnistes.
2. ) Neurones Biologiques
Le cerveau humain possède deux hémisphères latérales reliées par le corps calleux et d’autres ponts axonaux, il pèse moins de deux kilogrammes et contient mille milliards de cellules, dont 100 milliards sont des neurones constitués en réseaux.
2.1. ) Description
Les neurones sont des cellules nerveuses décomposables en 4 parties principales (Fig. 1) :
les dendrites, sur lesquelles les autres cellules entrent en contact synaptique : c’est par les dendrites que se fait la réception des signaux.
le corps de la cellule, c’est l’unité de traitement.
l’axone, où passent les messages accumulés dans le corps de la cellule : l’envoie de l’information se fait par l’axone.
les synapses par lesquelles la cellule communique avec d’autres cellules, ce sont des points de connexion par où passent les signaux de la cellule.
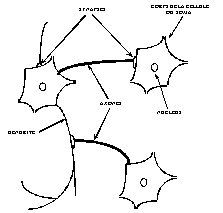
Fig. 1 : Exemple de réseau de neurones biologiques.
2.2. ) Communication entre neurones
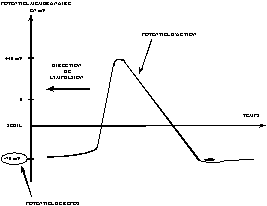
Un neurone stimulé envoie des impulsions électriques ou potentiels d’action, à d’autres neurones. Ces impulsions se propagent le long de l’axone unique de la cellule. Au point de contact entre neurones, les synapses, ces impulsions sont converties en signaux chimiques. Quand l’accumulation des excitations atteint un certain seuil, le neurone engendre un potentiel d’action, d’une amplitude d’environ 100mV et pendant une durée de 1ms (Fig. 2). Le neurone émettant le signal est appelé neurone pré-synaptique et celui recevant ce signal, neurone post-synaptique (Fig. 3).
|
|
|
Fig. 2 : potentiel d’action. |
Fig. 3 : propagation du potentiel d’action. |
2.3. ) Conclusion
Les propriétés physiologiques des neurones qui viennent d’être exposées ne reflètent pas la complexité de la réalité : seules les propriétés de base utilisées dans le cadre du connexionnisme de base sont décrites. Ces dernières sont exploitées dans le modèle formel proposé par MacCulloch et Pitts. Le neurone est considéré comme un automate à seuil, qui suivant une excitation et un certain seuil, répond ou non par un potentiel d’action.
3. ) Approches Formelles
C’est en 1943 que le premier modèle de neurone formel est proposé. Il s’inspire du neurone biologique : il possède un certain nombre d’entrées, similaires aux dendrites du neurone biologique, un corps servant d’unité de traitement, et un axone permettant la transmission d’un potentiel d’action à d’autres neurones.
3.1. ) Neurone formel
Le neurone formel est un modèle mathématique simplifié du neurone biologique, il présente un certain nombre d’entrées, les dendrites, un corps traitant les entrées suivant la méthode du tout ou rien, et un axone véhiculant la réponse du neurone.
3.1.1. ) Principes de fonctionnement
Chaque entrée est affectée d’un poids. Le passage des entrées dans le corps du neurone se fait en deux étapes. La première étape consiste à faire une somme pondérée des entrées par les poids respectifs des connexions sur lesquelles ces entrées se propagent. La seconde étape consiste à calculer l’image de cette somme pondérée par une fonction de transfert binaire. Le résultat obtenu provoque ou non le déclenchement d’un potentiel d’action suivant le dépassement d’un seuil, et sert à son tour d’entrée à d’autres neurones (Fig. 4).
3.1.2. ) Modélisation générale
Un neurone formel peut être défini par les cinq éléments suivants /DAVALO & al. 93/ :
- la nature de ses entrées
- la fonction d’entrée totale H définissant le pré-traitement effectué sur les entrées
- la fonction d’activation, ou d’état, F définissant l’état interne du neurone en fonction de son entrée totale.
- la fonction de sortie G calculant la sortie du neurone en fonction de son état d’activation.
- la nature de la sortie du neurone.
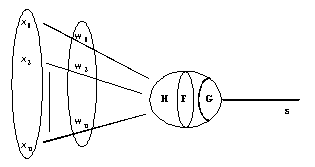
Fig. 4 : structure générale du neurone formel.
Les entrées et les sorties peuvent être binaires (-1 , +1) ou (0 , 1) ou réelles.
La fonction d’entrée totale peut être booléenne, linéaire ![]() ou affine
ou affine ![]() , polynomiale de degré supérieur à deux.
, polynomiale de degré supérieur à deux.
La fonction de sortie est en général considérée comme la fonction identité, la sortie du neurone est généralement considérée comme l’activation.
3.2. ) Les réseaux de neurones formels
Les réseaux de neurones artificiels regroupent en réseaux un certain nombre de neurones formels connectés entre eux de diverses manières.
Un réseau est défini par /NEDELLEC & al. 89/ :
- sa topologie, qui représente le type de connexion existant entre les divers neurones du réseau.
- la fonction de transfert qui caractérise le neurone.
- les méthodes d’apprentissage utilisées pour faire apprendre au réseau des couples d’entrées-sorties.
3.2.1. ) Les topologies
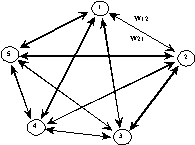
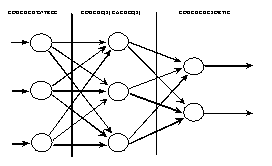
Les neurones sont connectés entre eux de diverses manières : réseaux totalement interconnectés (Fig. 8), réseaux à couches ou réseaux de type feedforward (Fig. 9), réseaux récurrents (Fig. 10) ...
|
|
|
|
Fig. 8 : réseau totalement interconnecté. |
Fig. 9 : réseau à couches. |
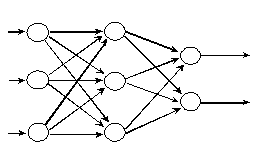
Fig. 10 : réseau récurrent.
3.2.2. ) Les fonctions de transfert
Les fonctions de transfert les plus couramment utilisées sont / DAVALO & al. 93/ (Fig. 11) :
- la fonction binaire (Fig. 11 a°)).
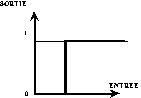
- la fonction seuil (Fig. 11 b°)) :
- la fonction sigmoïde
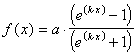 (Fig. 11 d°)).
(Fig. 11 d°)). - une fonction stochastique :
- toute fonction, généralement choisie croissante et impaire.
S(X) = X, si X appartient à [U , V]
S(X) = U, si X U
S(X) = V, si X V
ou multi-seuils (Fig. 11 c°)).
F(X) = 1, avec la probabilité 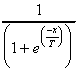
F(X) = 0, sinon.
T est la température, lorsqu’elle tend vers zéro, la fonction tend vers la fonction seuil.
|
a°) Fonction de Heaviside, utilisée par Mc Culloch et Pitts. |

b°) fonction linéaire à seuil. |
|
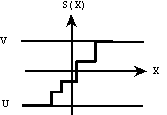
c°) fonction linéaire multi-seuils. |
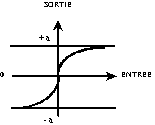
d°) fonction sigmoïde. |
Fig. 11 : exemples de fonctions de transfert.
3.2.3. ) Types d’apprentissages
Il existe deux types d’apprentissages : l’apprentissage supervisé et l’apprentissage non supervisé :
apprentissage supervisé : un superviseur, ou professeur, fournit au réseau des couples d’entrées-sorties. Il fait apprendre au réseau l’ensemble de ces couples, par une méthode d’apprentissage, comme la rétro-propagation du gradient de l’erreur, en comparant pour chacun d’entre eux la sortie effective du réseau et la sortie désirée. L’apprentissage est terminé lorsque tous les couples entrée-sortie sont reconnus par le réseau. Ce type d’apprentissage se retrouve, entre autres, dans le perceptron.
apprentissage non supervisé : cet apprentissage consiste à détecter automatiquement des régularités qui figurent dans les exemples présentés et à modifier les poids des connexions pour que les exemples ayant les mêmes caractéristiques de régularité provoquent la même sortie /BOURRET & al. 91/. Les réseaux auto-organisateurs de Kohonen sont les réseaux à apprentissage non supervisé les plus connus.
3.2.4. ) Les méthodes d’apprentissage
Dans les systèmes experts, les connaissances de l’expert ont une forme énumérée : elles sont exprimées sous forme de règles. Dans le cas des réseaux de neurones, les connaissances ont une forme distribuée : elles sont codées dans les poids des connexions, la topologie du réseau, les fonctions de transfert de chaque neurone, le seuil de ces fonctions, la méthode d’apprentissage utilisée. Il existe un certain nombre de méthodes d’apprentissage :
la règle de Hebb : c’est la méthode d’apprentissage la plus ancienne (1949), elle est inspirée de la biologie. Elle traduit le renforcement des connexions liant deux neurones activés. Si un des deux neurones au moins n’est pas activé, le poids de la connexion n’est pas modifié /DAVALO & al. 93/.
la rétro-propagation du gradient de l’erreur : cet algorithme est utilisé dans les réseaux de type feedforward, ce sont des réseaux de neurones à couches, ayant une couche d’entrée, une couche de sortie, et au moins une couche cachée. Il n’y a pas de récursivité dans les connexions, et pas de connexions entre neurones de la même couche. Le principe de la rétro-propagation consiste à présenter au réseau un vecteur d’entrées, de procéder au calcul de la sortie par propagation à travers les couches, de la couche d’entrée vers la couche de sortie en passant par les couches cachées. Cette sortie obtenue est comparée à la sortie désirée, une erreur est alors obtenue. A partir de cette erreur, est calculé le gradient de l’erreur qui est à son tour propagé de la couche de sortie vers la couche d’entrée, d’où le terme de rétro-propagation. Cela permet la modification des poids du réseau et donc l’apprentissage. L’opération est réitérée pour chaque vecteur d’entrée et cela jusqu’à ce que le critère d’arrêt soit vérifié.
les algorithmes génétiques : ils représentent une modélisation de la sélection naturelle /GOLDBERG 94/. Une population d’individus est générée aléatoirement. Un certain nombre d’individus répondant le mieux aux critères de sélection est choisi. A partir de cette population d’élites, une nouvelle population est générée par reproduction, mutation, ou crossover sur les individus de départ, ou parents. L’opération est recommencée jusqu’à la vérification du critère d’arrêt.
Algorithme de Sollis et Wets : c’est une méthode stochastique d’optimisation /GLORENNEC 94 b/ . Soit M un vecteur contenant l’ensemble des paramètres à optimiser. Soit G un vecteur de bruit gaussien. Ce dernier sera chargé de faire évoluer les paramètres à optimiser par somme ou différence avec le vecteur M. Soit B un vecteur de biais contenant la moyenne de G, il mémorisera les réussites de la minimisation de la fonction de coût. Cette méthode converge avec une probabilité de 1 vers le minimum global.
3.3. ) Le perceptron
La conception du perceptron par Rosenblatt marque la naissance historique du connexionnisme dans les années 50 /DAVALO & al. 93/. Le perceptron élémentaire est constitué d’un réseau d’associateurs linéaires, basés sur la représentation mathématique de la cellule nerveuse réalisée par McCulloch et Pitts et ayant pour technique d’apprentissage la loi de Widrow-Hoff.
3.3.1. ) Description
Les perceptrons sont des réseaux de type feedforward, possédant la structure suivante : une couche de connexions fixes, située entre les unités d’entrée, la rétine, et les unités d’association. La seconde couche relie les unités d’association et les unités de réponse : c’est sur ces poids que l’adaptation agit. Dans le perceptron, il n’y a qu’une seule couche qui varie en fonction de l’adaptation (Fig. 12).
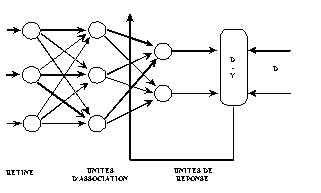
Fig. 12 : schéma descriptif du perceptron mono-couche.
La fonction de transfert utilisée pour chaque neurone est la fonction binaire (Fig. 11 a°)).
Seules les connexions entre les unités d’association et les unités de réponse sont affectées d’un poids qui est modifié par la règle d’apprentissage.
L’apprentissage peut-être basé sur la loi de Widrow-Hoff, ou la règle de Hebb.
C’est un réseau à apprentissage supervisé.
3.3.2. ) Limites
La fonction de transfert utilisée étant binaire, les sorties du réseau seront limitées à deux valeurs.
Si une des entrées est distante des autres, du point de vue euclidien, la convergence du réseau risque d’être ralentie.
Le perceptron ne peut classer que des données linéairement séparables, problème du xor (ou exclusif) (Fig. 13).
La recherche connexionniste a été brutalement avortée par la parution d’un livre démontrant les limites théoriques du perceptron /DAVALO 93/. Cette interruption a favorisé les recherches dans le domaine de l’intelligence artificielle et des systèmes experts.
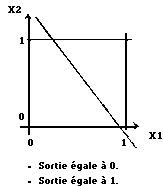 |
|
Fig. 13 : problème du xor.
3.4. ) Les réseaux de neurones récurrents
Le perceptron ne possède pas de liaison récurrente, il représente la première application de réseau de neurones de McCulloch et Pitts. Les limites du modèles du perceptron ont amené les chercheurs à proposer d’autres modèles avec des topologies différentes. Hopfield, dans les années 80, propose un modèle inspiré de la physique, les verres de Spin /MEZART & al. 91/, et relance la recherche neuronale.
3.4.1. ) Architecture de Hopfield
Les réseaux de Hopfield sont des réseaux de neurones totalement interconnectés, récursifs. Il n’y a plus de notions de couche comme dans le perceptron. Les réseaux de neurones récurrents et auto-récurrents permettent d’obtenir des résultats intéressants comparativement aux réseaux à couche.
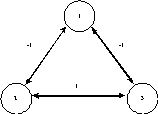
Fig. 18 : exemple de réseau récurrent symétrique.
La fonction de transfert utilisée est une fonction binaire à seuil nul telle que :

Il existe 2 types d’approche dans la dynamique des réseaux récurrents /BOURRET & al. 91/ :
- les dynamiques asynchrones séquentiellement, des neurones sont mis à jour suivant la règle de Mac Culloch et Pitts les uns après les autres.
- les dynamiques synchrones, à chaque itération tous les neurones effectuent simultanément leur mise à jour.
3.4.2. ) Architecture de LAPEDES-FARBER
Dans la Fig. 19, l’activation a(t) est une fonction linéaire des entrées du neurone, la sortie est une fonction non linéaire de la fonction d’activation. f ( . ) est une fonction non linéaire /TSOÏ & al. 94/. La sortie se calcule comme suit :
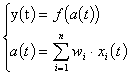 , où les xi sont les entrées et les wi sont des constantes.
, où les xi sont les entrées et les wi sont des constantes.
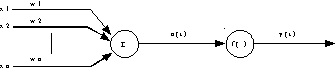
Fig. 19 : architecture de Lapedes-Farber.
Dans la Fig. 20, le feedback se fait au niveau de l’activation.

Fig. 20 : architecture avec feedback au niveau de l’activation.
3.4.3. ) Architecture de BACK-TSOÏ
Dans la Fig. 21, chaque fonction synaptique, c’est à dire les poids, est modélisée par des fonctions de transfert linéaires, avec des pôles et des zéros /TSOÏ & al. 94/ :
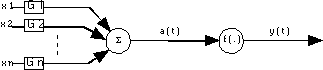
Fig. 21 : architecture avec feedback au niveau de la synapse.
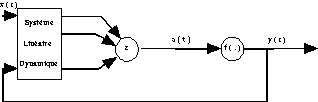
Fig. 22 : architecture avec feedback local au niveau de la sortie.
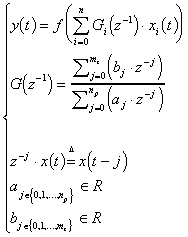
L’architecture de Lapedes-Farber peut être considérée comme un cas particulier de l’architecture de Back-Tsoï. Dans le cas de Lapedes-Farber la fonction de transfert synaptique contient uniquement des zéros : ![]() .
.
3.4.4. ) Architecture de FRASCONI-GORI-SODA
Dans cette architecture, la boucle de retour de la sortie possède des retards en cascade (Fig. 23) /TSOÏ & al. 94/ :
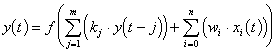 .
.
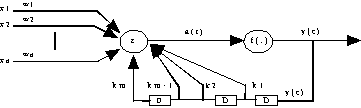
Fig. 23 : architecture de Frasconi-Gori-Soda.
Une généralisation de cette structure se fait par le remplacement des retards dans la boucle de retour par une fonction de transfert avec des pôles et des zéros (Fig. 24) :
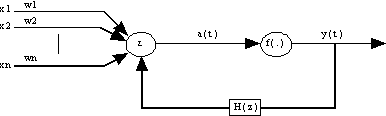
Fig. 25 : architecture de Frasconi-Gori-Soda généralisée.
La fonction de transfert H(z) possède des pôles et des zéros :
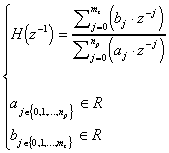
3.5. ) Conclusion
Les réseaux de neurones de type feedforward sont les plus anciens et les plus connus : perceptron, adaline. Un certain nombre de structures neuronales récurrentes ont été proposées notamment par Hopfield en 1982. Ces architectures possèdent des propriétés de mémoire associative /REMY 19XX/, et permettent la reconnaissance de forme. Le bouclage de la sortie sur l’entrée permet de prendre en compte la non-linéarité introduite par la fonction de transfert du neurone.
4. ) La Commande Neuronale
En commande de processus, le neuronal, comme le flou, n’a pas besoin de modèle analytique du processus à commander. Cette caractéristique se révèle intéressante dans le cas de modèles non linéaires difficilement modélisables mathématiquement. Il s’agit de faire de la commande de processus par un réseau de neurones.
4.1. ) Principe
Un dilemme se pose lorsqu’il s’agit de faire de la commande neuronale : d’où proviennent les informations concernant le contrôle du processus, sachant que c’est le réseau lui même qui doit les produire /BARTO 89/. Pour résoudre ce problème, un certain nombre de solutions existent.
4.2. ) Solutions
Copier un régulateur déjà existant. L’intérêt de cette méthode ne semble pas évident. En effet pourquoi copier un régulateur qui existe déjà ? Il existe deux cas où cette copie d’un régulateur par un réseau de neurones est intéressante. Le premier cas se présente lorsque ce régulateur est un être humain. Le deuxième cas est celui où le réseau peut réguler le processus à partir d’un modèle moins difficile à évaluer que celui qui est demandé par le régulateur habituel.
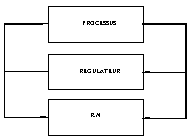
Fig. 23 : copie d’un régulateur.
D’autres utilisations possibles des réseaux de neurones dans l’identification et la prédiction :
- La prédiction adaptative.
- Identification du processus.
- Identification du processus inverse.
|
|
|
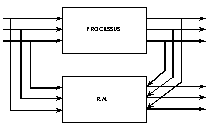
a°) identification du processus |
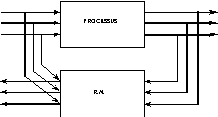
b°) identification du processus inverse |
Fig. 24 : utilisation d’un réseau de neurones dans l’identification d’un processus.
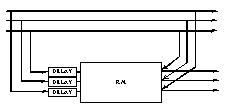
Fig. 25 : prédiction adaptative.
4.3. ) Conclusion
Dans un réseau de neurones toute la connaissance est répartie dans la topologie du réseau, le poids des connections synaptiques, les fonctions de transfert utilisées, les biais. De l’algorithme d’apprentissage dépend aussi l’apprentissage de la connaissance. Les capacités d’apprentissage des réseaux de neurones et leur propriété d’approximateur universel /N’GUYEN 94/, /TSOI & al. 94/ leur confèrent un intérêt tout particulier dans le domaine de l’identification et le contrôle de procédés : un réseau de neurones peut par exemple apprendre le comportement d’un système non linéaire, difficile à modéliser par les méthodes classiques d’identification. L’inconvénient est l’impossibilité de savoir comment cela fonctionne à l’intérieur de cette boîte noire.
5. ) Conclusion
Dans le cerveau humain, les neurones recueillent les signaux provenant d’autres neurones grâce aux structures arborescentes que sont les dendrites, et ils émettent des impulsions électriques le long de l’axone, qui se ramifie en plusieurs milliers de terminaisons. A chaque terminaison se trouve une structure nommée synapse, qui transforme le signal électrique propagé dans l’axone en signaux électriques inhibant ou non le neurone post-synaptique. Lorsqu’un neurone est plus activé qu’inhibé, il « décharge », c’est à dire qu’il émet une impulsion électrique dans son propre axone. L’apprentissage résulte d’une modification de l’efficacité des synapses, modulant ainsi l’influence des neurones les uns sur les autres.
Dans un réseau de neurones formels, chaque neurone recueille des valeurs réelles, ou binaires provenant d’autres neurones grâce à ses connections. En général toutes ces valeurs sont ajoutées, et passent par une fonction d’activation qui calcule la valeur de sortie du neurone. Cette valeur, à son tour, se propage vers les autre neurones du réseau, jusqu’à leur sortie respective.
Les réseaux de neurones possèdent des propriétés d’apprentissage intéressantes, de reconnaissance de forme, d’approximateur universel. Les inconvénients ne sont pas négligeables, citons notamment le nombre de poids à optimiser, le choix de la structure du réseau, le choix des fonctions de transfert, les performances de la règle d’apprentissage.